Modelo de Solow

Al inicio los clásicos, con Adam Smith a la cabeza, atribuyen el crecimiento económico a la mano invisible del mercado.

En contraposición a ellos, los neoclásicos proponen otra teoría, ideada por Robert Solow en la década de 1950, según la cual un incremento sostenido en la inversión genera crecimiento solo de forma temporal: la relación entre capital y trabajo (K/N) disminuye, la productividad Marginal del Capital cae lo que lleva a que la economía se mueva hacia una senda de crecimiento a largo plazo; entonces la producción aumentará en la misma proporción en la que crece la fuerza de trabajo (esto sería ajustado en versiones posteriores), más un factor para reflejar las mejoras en la productividad (o en el avance tecnológico).

Modelo aplicando ecuación Cobb-Douglas (con avance tecnológico)

Entonces, partimos de la función de producción asumiendo tres fuentes para el crecimiento económico: fuerza de trabajo N, capital K y avance tecnológico A, las cuales definen el producto Y.

Y = A F(K,N)

Asumiendo una curva Cobb-Douglas, en donde la participación de los recursos asignados a fuerza de trabajo (salarios, sueldos, etc.) respecto al total de la renta es 1 - Φ y la participación del capital respecto a la renta es Φ:

Y = AK ^Φ N^1-Φ

Luego obtenemos la tasa de variación ΔY/Y que representa el crecimiento económico; así para cada factor:

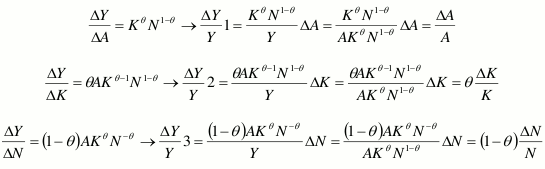
Y sumando todas las tasas de cambio, obtenemos la tasa total de cambio o de crecimiento de la producción:

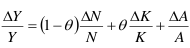
Modelo de Solow caso per cápita

Ahora, pasando a un análisis per cápita, primero obtenemos el producto per cápita y:

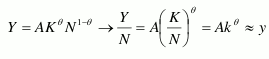
Luego obtenemos la tasa de cambio:

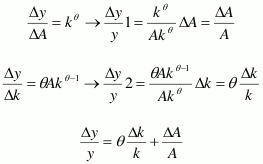
Ahora, si en este punto adoptamos la terminología marxista, podríamos definir a K como el capital constante c, N como el capital variable v y la relación c / v = Composición Orgánica de Capital₇, es K/N = k = c/v = COK , entonces obtenemos que:

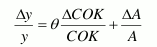
En conclusión, el producto per cápita aumenta en relación directa al incremento de la Composición Orgánica de Capital y como Θ 8.

Residuo de Solow

Algunos autores definen A como la productividad Marginal de todos los factores, y debido a que
los factores y los productos son observables pero A no lo es, entonces simplemente se da vuelta a
la ecuación de la tasa de crecimiento, y a esto se le conoce como residuo de Solow:

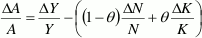
Inversión, ahorro y estado estacionario

Recordando lo anteriormente anotado, dijimos que el crecimiento en el nivel de inversión genera
crecimiento durante un periodo limitado nada más, esto se debe a que el nivel de inversión se
encuentra íntimamente ligado a la COK y al nivel de ahorro.

El estado estacionario se refiere que Δ COK = 0, y si además vemos que Δ COK = Δ neta capital per cápita k = Ahorro – inversión por crecimiento de N y depreciación de K, entonces el estado estacionario se cumple cuando el nivel de ahorro es igual al de inversión productiva, entonces cualquier incremento de la inversión a corto plazo genera crecimiento pero a largo plazo si no se incrementa la tasa de ahorro el nivel de producción per cápita volverá a ser el mismo. Pero como Δ COK = 0 puede cumplirse cuando Δ K = Δ N, entonces el total de la producción crecerá a la misma tasa a la que crezca la masa salarial (algunos autores hablan del crecimiento poblacional).

En conclusión: la tasa de crecimiento correspondiente al estado estacionario no depende de la tasa de ahorro, sino de la variación de la masa salarial.

Autor: John Cajas

7 - Recordando que, bajo el marxismo, capital C es toda suma de valores que buscan un plusvalor vía explotación de fuerza de trabajo, entonces este capital se compone de c: capital constante, que es el gasto en medios de producción, el cual no genera valor; y v: capital variable, que es el gasto en fuerza de trabajo, la cual genera el plusvalor. Así: C = c+v
8 - Este puede ser un interesante punto a favor de la ley tendencial de la tasa de ganancia expuesta por Marx en el libro III de El Capital.