Ejemplo de Función de Producción

A continuación presentaremos algunos ejemplos de funciones de producción.

Ejemplo de Función de Producción Linear

Comenzamos por el caso mas simple, la función de producción linear con un solo factor de producción. Por ejemplo, la función de producción de una máquina a la que se le puede introducir plástico y produce un muñeco de plástico. Por cada kilo de plástico, produce 50 muñecos.

​​

En este ejemplo, la función de producción es:

Q = 50 P 

Donde Q es la cantidad de muñecos producida y P los kilos de plástico.

El gráfico de esta función de producción es el siguiente:

Ejemplo de Función de Producción con Rendimiento Marginal Decreciente 

Este caso se trata una extensión del ejemplo anterior: una función de producción de un solo factor, pero incorporando el rendimiento marginal decreciente.

Por ejemplo, supongamos que en un taller, la primer persona es capaz de producir 100 mesas por día, la segunda no producirá 100, sino que menos, porque el rendimiento es decreciente. En este ejemplo vamos a suponer que la función de producción es:

Q = 100 * L^0.95

^​Por lo tanto, la segunda persona producirá 93, la tercera 91 y así sucesivamente:

 

Personas	Producción	Producto Marginal
1	100	100
2	193	93
3	284	91
4	373	89
5	461	88
6	549	87
7	635	87
8	721	86
9	806	85
10	891	85

 

El gráfico de este ejemplo de función de producción es:

En color verde vemos el producto marginal, que es decreciente en este ejemplo. 

Ejemplo: Función de Producción con Múltiples Factores

En los 2 ejemplos anteriores vimos funciones de producción con un solo factor, en este ejemplo, vamos a ver una función de producción con múltiples factores:

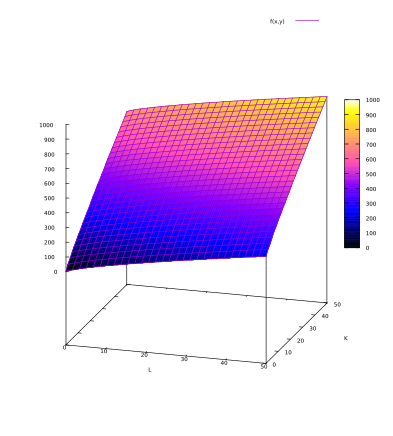
Q = A*L^0.8 + B*K^0.9

Se trata de una función de producción todavía muy rudimentaria, porque los factores de producción no interactúan entre sí. Cada factor de producción tiene rendimientos marginales decrecientes. Este ejemplo podría describir una situación en la que personas pueden ser susitutídas por robots, y las personas y los robots no interactúan entre sí. 

Si el primer robot tiene una productividad que es el doble que la de las personas, B = 2A

Este ejemplo también muestra que la productividad marginal de los robots es mayor que la de las personas (0.9 > 0.8) para cantidades similares. Puede servir para describir una situación real.  

El gráfico de este ejemplo es:

Ejemplo: Función de Producción Cobb Douglas

La función de producción Cobb Douglas es una de las mas conocidas porque sirve en los modelos económicos para describir muchas situaciones de producción agregadas, además de que tiene ciertas propiedades que la hacen muy útiles para elaborar modelos econométricos. 

La forma de la función de producción Cobb Douglas es:

Q(K,L) = A L ^β K ^α​

Donde 
L: trabajo
K: capital

Se trata de una función de producción con 2 factores, con rendimientos marginales decrecientes. El producto marginal es positivo y decreciente. La elasticidad de producción es constante.

Por ejemplo:

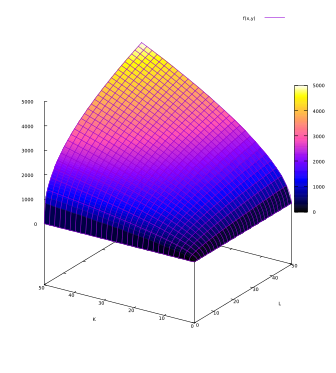
Q = 100 L^0.4 K^0.6

En este caso, tiene rendimiento constantes a escala porque  β + α = 1 

El gráfico de este ejemplo es:

Ejemplo: Función de Producción con factores en proporciones fijas

La función de producción de proporciones fijas es muy conocida en economía. Se trata de una función de producción que utiliza factores de proporción en una determinada proporción. Por ejemplo, una persona por cada computadora, 2 dos personas por un camión, etc. 

Si se modifica la cantidad utilizada de un factor de producción sin modificar el otro, la cantidad producida no se modifica. 

Este tipo de función de producción se puede representar matemáticamente por la siguiente fórmula:

Q = min {aL,bK}

Por ejemplo, si se necesita una persona por computadora, a=b. Puede ser:

Q = 100 min {L,K}

Ejemplo: Factores de Producción Sustitutos Perfectos

En este ejemplo, un factor puede ser sustituido por otro en determinada proporción sin que se modifique la cantidad producida. 

Por ejemplo, si un robot puede sustituir a dos personas.

En este caso, la función de producción puede ser:

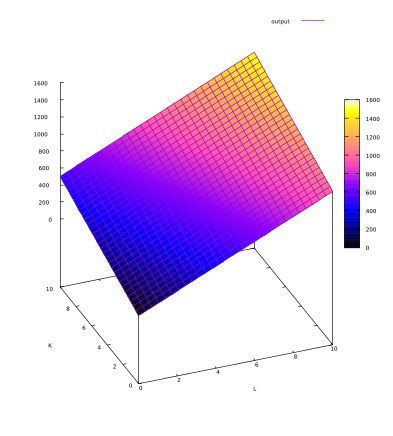
Q = 100 L + 50 K 

L: personas
K: robots

El gráfico de este ejemplo es: